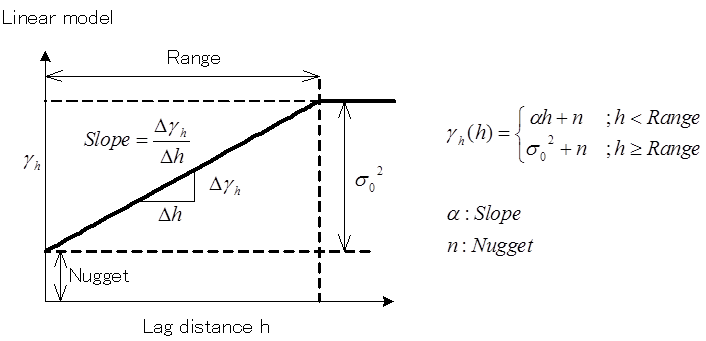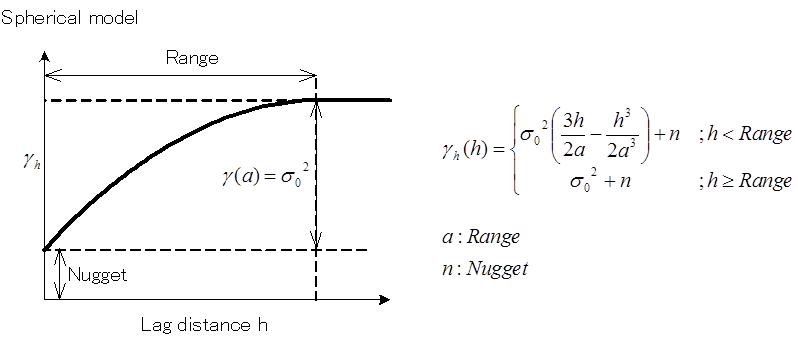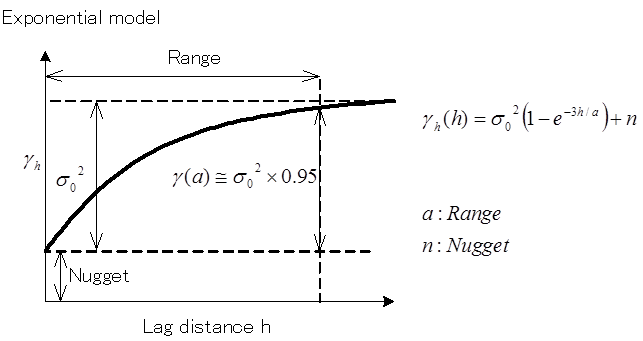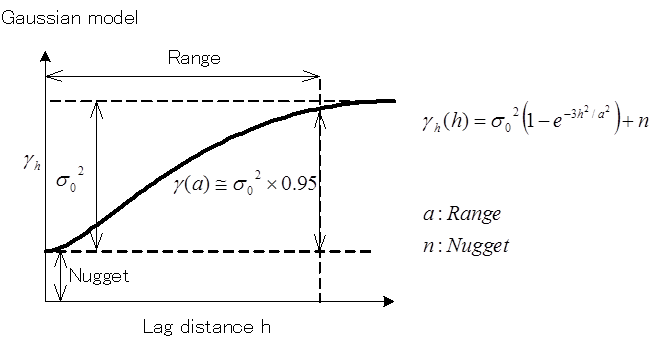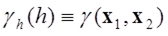
いわゆるKriging法の考え方は、補間対象とする変数は3つの成分(地域的に固定的な成分、地域的な相関を有するノイズ成分、地域的な相関を持たないノイズ成分)から構成されるとして、それを確率変数ととらえて地域性を反映した補間を行うものです。これを実地応用する場合には、Simple Kriging, Ordinary Kriging, Universal Kriging, Block Krigingなどの手法があります。NK-GIASが用意する方法はOrdinary Krigingにあたります。(注:次のバージョンで更新予定)
Ordinary Krigingは補間対象とする変数の、空間的(地域的)に固定的な成分を無視して単純化したものです。空間的に相関性を持つ成分の表現は次式のように2点間の距離の関数として表現します。
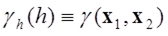
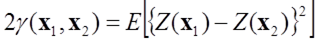
ここに、
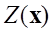 : 補間対象とする変数の位置
: 補間対象とする変数の位置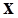 における値
における値
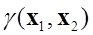 : 位置
: 位置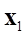 と
と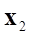 の間の
の間の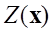 のsemivariance(分散値の半分)
のsemivariance(分散値の半分)
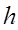 : 位置
: 位置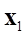 と
と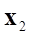 の間の距離
の間の距離
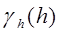 : semivariogram
: semivariogram
このような式で表現される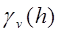 をvariogramと呼びます。variogramは下図のような概念で規定することとします。“Nugget”は距離ゼロにおけるsemivarianceで、他は距離の関数として一意に定めます。この関数形はある距離に達するとほぼ一定の値 “Sill”に近づくとして、そのときの距離を“Range”と呼ぶこととします。
をvariogramと呼びます。variogramは下図のような概念で規定することとします。“Nugget”は距離ゼロにおけるsemivarianceで、他は距離の関数として一意に定めます。この関数形はある距離に達するとほぼ一定の値 “Sill”に近づくとして、そのときの距離を“Range”と呼ぶこととします。
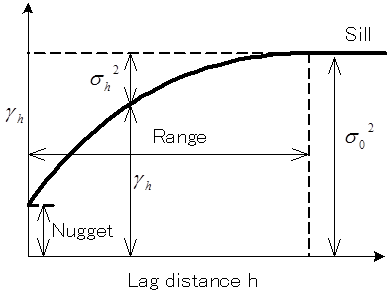
補間対象となる地点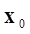 (
(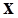 は位置ベクトルを表す)の推定値(補間結果)
は位置ベクトルを表す)の推定値(補間結果)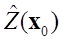 は、その補間に用いるデータ地点数を
は、その補間に用いるデータ地点数を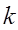 として、次式のような行列式で求めます。
として、次式のような行列式で求めます。
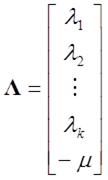 ,
, 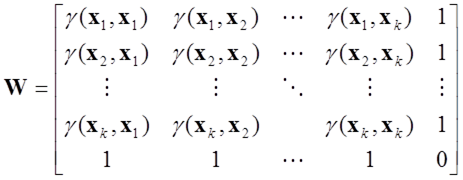
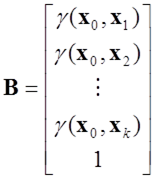 ,
, 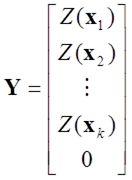
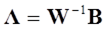
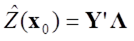 ,
, 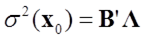
ここに、
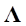 : データ地点行列
: データ地点行列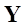 のそれぞれに関する重み係数
のそれぞれに関する重み係数
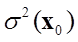 : 補間結果の推定分散値
: 補間結果の推定分散値
NK-GIASではvariogramの関数として、“Linear”, “Spherical”, “Exponential”, “Gaussian”の4つの関数形を用意しています。